BAB FUNGSI MATEMATIKA DISKRIT

  TUGAS
Nama         : Naufal Farid
Nim            : A11.2011.05895
Mata Kuliah: Matematika Diskrit

  Dalam matematika diskrit konsep fungsi sangat penting, dimana fungsi merupakan relasi yang mempunyai syarat setiap anggota dari daerah definisi (domain) mempunyai pasangan tepat satu anggota dari daerah Hasil (codomain).

DEFINISI FUNGSI

Diberikan dua himpunan A dan B, relasi biner f dari himpunan A ke B merupakan suatu fungsi jika setiap elemen di dalam himpunan A mempunyai pasangan tepat satu elemen himpunan B.
Apabila f adalah fungsi dari himpunan A ke B maka notasi fungsinya
f : A → B
Himpunan A disebut daerah definisi(domain) dan himpunan B disebut daerah hasil (codomain).
Untuk x ∈ A dan y ∈B maka rumus fungsí 1) dapat dinyatakan sbb:
x → y = f(x)

Terapan Fungsi
1. Formula pengisian nilai dalam bahasa pemrograman dinyatakan dengan assignment
Contoh diberikan rumusan fungsi f(x) = x2 +1 , f(x) = x +1 , apabila tidak didefinisikan secara khusus tentang daerah definisi maka daerah definisi dan daerah hasil adalah himpunan Himpunan bilangan riil misal R.
Dalam himpunan pasangan terurut fungsi didefinisikan sbb:
f = { (x1, x2}/ x ∈ R }

2. Kode program ( source code)
Fungsi yang dispesifikasikan dalam bahasa Pascal
Function abs(x: integer): integer;
Begin
if x < 0 then
abs := -x
else
abs := x;
end;

Relasi f = {(1,a),(2,b),(3,c) }dari himpunan A ke B, {1,2,3} ∈ A dan {a,b,c}∈ B merupa- kan fungsi karena Relasi f memasangkan tepat satu anggota himpunan A dengan anggota himpunan B
Keterangan :
f(1) = a, f (2) = b dan f (3) = c
Himpunan A disebut daerah definisi dan himpunan B sebagai daerah hasil.

JENIS FUNGSI

Ditinjau pada daerah hasil atau bayangan fungsi dibedakan atas fungsi injektif(injective), surjektif( surjective) dan bijeksi (bijection)

Fungsi injektif (injective)
 Fungsi f dikatakan one-to-one atau injektif (injective) apabila a dan b anggota himpunan A maka f(a) ≠ f(b) bilamana a ≠ b untuk f(a) dan f(b) anggota himpunan B.

Fungsi surjektif(surjective)
 Fungsi f dikatakan pada (onto) atau surjektif(surjective) apabila setiap elemen dari himpunan B merupakan bayangan dari satu atau lebih elemen himpunan A.Dengan kata lain seluruh elemen himpunan B merupakan jelajah dari f.

Fungsi bijeksi(bijection)
 Fungsi f dikatakan berkorespodensi satu-satu atau bijeksi(bijection) apabila ia fungsi one-to-one dan surjective.

FUNGSI INVERS
Apabila f merupakan fungsi berkorespondensi satu-satu dari himpunan A ke himpunan B maka fungsi tersebut mempunyai invers yaitu f -1(y) = x , untuk x ∈ A dan y ∈ B, f -1 merupakan invers dari fungsi f.

KOMPOSISI FUNGSI
Komposisi dari dua fungsi f dan g dinyatakan f°g, f merupakan fungsi yang memetakan anggota himpunan A ke himpunan B dan fungsi g memetakan anggota himpunan B ke himpunan C. Fungsi dari himpunan A ke himpunan C didefinisikan f° g(x) = f( g(x)), x ∈ A .

Beberapa Fungsi Khusus
Beberapa fungsi khusus yang sering digunakan dalam bahasa pemrograman seperti fungsi floor, ceiling, modulo, faktorial, perpangkatan dan logaritmik.
1.Fungsi floor dan ceiling
Fungsi ini diperlukan untuk membulatkan ke bawah dan keatas. Fungsi floor diperlukan untuk membulatkan nilai pecahan kebawah, misalkan x bilangan riil maka bilangan floor dilambangkan ⎣x⎦. Fungsi ceiling diperlukan untuk membulatkan nilai pecahan keatas dan dilambangkan ⎡x⎤.

2.Fungsi Modulo
Fungsi modulo adalah fungsi dengan operator mod, misalkan b sembarang bilangan bulat dan m bilangan bulat positip maka b mod memberikan sisa pembagian bilangan bulat apabila b dibagi dengan m .

3.Fungsi hash
Misalkan dipunyai sel-sel pada memori komputer yang diberi indek dari 0 sampai dengan 10.

4.Fungsi faktorial
Untuk sembarang bilangan bulat non negatif n, faktorial dari n dilambangkan dengan n ! yang didefinisikan.

BAB LOGIKA MATEMATIKA DISKRIT

 TUGAS
Nama         : Naufal Farid
Nim            : A11.2011.05895
Mata Kuliah: Matematika Diskrit


LOGIKA adalah cara berpikir dengan mengembangkan sesuatu berdasarkan akal budi bukan dengan perasaan atau pengalaman.

Fakta1

Anak gaul menggemari smash

Fakta2

Wibisono adalah anak gaul

Wibisono menggemari smash

#PROPOSISI

 Proposisi adalah kalimat deklaratif yang bernilai benar (true) atau salah (fals), tetapi tidak dapat sekaligus keduanya. Kebenaran atau kesalahan dari sebuah kalimat disebut nilai kebenaran (truth value).

p : Australia beribukota Sidney

p bernilai 0 (SALAH)

q : Rumput adalah tumbuhan

q bernilai 1 (BENAR)

* Memadukan Proposisi

Operator Logika untuk menkombinasikan proposisi yaitu dan (and), atau (or) dan tidak (not).
Proposisi yang terbentuk dari pengkombinasian beberapa proposisi atomik disebut proposisi majemuk

.KONJUNGSI

Contoh :

p : Hari ini hujan

q : Hari ini dingin

p Λ q : Hari ini hujan dan hari ini dingin / hari ini hujan dan dingin

Konjungsi p Λ q bernilai benar jika p dan q keduanya benar, selain itu nilainya salah

 

.DISJUNGSI

p : ibu pergi ke pasar

q : ibu belanja sayuran

p v q : ibu pergi ke pasar atau belanja sayuran

Disjunsi p v q bernilai salah jika p dan q keduanya bernilai salah,selain itu nilainya benar.

.INGKARAN

p : pemuda itu tinggi

~p : tidak benar pemuda itu tinggi / pemuda     

       itu tidak tinggi.

Ingkaran p bernilai benar jika p salah, sebaliknya bernilai salah jika p benar.

   

IMPLIKASI
p:IP mu diatas 3,5
q:Kamu dapat sepeda motor
 p -> q

Jika p maka q , Bila p terjadi maka q juga terjadi ,Tidak mungkin peristiwa p terjadi tapi peristiwa q tidak terjadi

 

BIIMPLIKASI 

p : IP-mu di atas 3,5

q : Kamu dapat sepeda motor

p <-> q

hanya jika p maka q

q terjadi jika dan hanya jika p juga terjadi

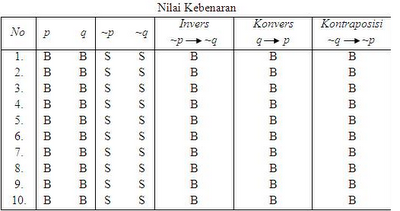
INVERS

p: Budi naik kelas

q: Budi dibelikan sepeda motor

~p → ~q

KONVERS 

p: Budi naik kelas

q: Budi dibelikan sepeda motor

q → p

KONTRAPOSISI 

p: Budi naik kelas

q: Budi dibelikan sepeda motor

~q → ~p

TAUTOLOGI

KONTRADIKSI

             Hukum Komutatif

p Λ q ≡ q Λ p

p V q ≡ q V p

          

          Hukum Asosiatif

(p Λq) Λ r ≡ p Λ(q Λr)

(p V q) V r ≡ p V (q V r)

Hukum Distributif 

p Λ(q V r) ≡ (p Λq) V (p Λr)

p V (q Λr ) ≡ (p V q) Λ(p V r) 

 Hukum Identitas 

            p Λ B ≡ p 

            p V S ≡ p

 Hukum Ikatan

  p V B ≡ T 

  p Λ S ≡ F